Maths XI-XII
The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society. Senior Secondary stage is a launching stage from where the students go either for higher academic education in Mathematics or for professional courses like Engineering, Physical and Biological science, Commerce or Computer Applications. The present revised syllabus has been designed in accordance with National Curriculum Framework 2005 and as per guidelines given in Focus Group on Teaching of Mathematics 2005 which is to meet the emerging needs of all categories of students. Motivating the topics from real life situations and other subject areas, greater emphasis has been laid on application of various concepts


The broad objectives of teaching Mathematics at senior school stage intend to help the students:
to acquire knowledge and critical understanding, particularly by way of motivation andvisualization, of basic concepts, terms, principles, symbols and mastery of underlyingprocesses and skills.
to feel the flow of reasons while proving a result or solving a problem.
to apply the knowledge and skills acquired to solve problems and wherever possible, bymore than one method.
to develop positive attitude to think, analyze and articulate logically.
to develop interest in the subject by participating in related competitions.
to acquaint students with different aspects of Mathematics used in daily life.
to develop an interest in students to study Mathematics as a discipline.
to develop awareness of the need for national integration, protection of environment,observance of small family norms, removal of social barriers, elimination of genderbiases.
to develop reverence and respect towards great Mathematicians for their contributionsto the field of Mathematics.
Pattern of Studies
● Interactive Classes
● Home Assignments
● Class Notes
● Periodic Class Tests
● Student's Monthly Report
● One to One Attention
● Doubt Classes
● Syllabus Revision
Report Analysis Parameters
● Tests Marks
● Attendance
● Class Discipline
● Class Response
● Home Assignments
● Student's Comparison with Class
● Last 3 Months Performance
● Special Remarks
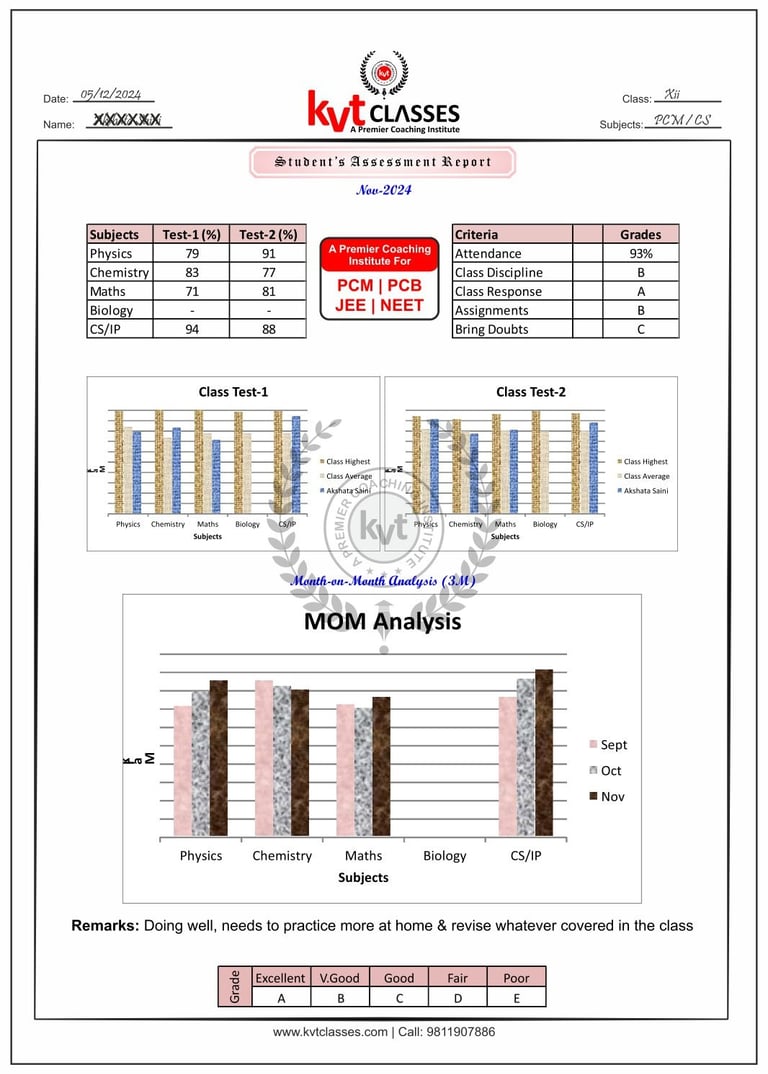
Student's Sample Report
Class Tests
● Two tests per subject in a month
● Test schedule on Saturday in extra hours
● Result within 1 week of test conduct
● Test discussion on result day
● Mistakes rectification briefing
Conduct of Classes
● On board explanation with notes
● Make Concept clear with practical examples
● Interactive class sessions
● Home work / Assignment at the end of the class
● Home work / Assignment check in the next class
● Quick recap of previous class in the next class
● Two tests per month/subject on Saturdays
● Class duration 1 Hr/sub alternate days (3Hrs./wk)
● Extra classes provided when needed
Classes Schedule 2024-25
Science Students Class XI-XII
Note: Class Tests will be conducted on Saturday in extra hours
Syllabus & Marks Weightage [ Class-XI ]
Syllabus & Marks Weightage [ Class-XII ]
Unit-I: Sets and Functions
1.Sets(20)Periods
Sets and their representations, Empty set, Finite and Infinite sets, Equal sets, Subsets, Subsets of a set of real numbers especially intervals (with notations). Universal set. Venn diagrams. Union and Intersection of sets. Difference of sets. Complement of a set. Properties of Complement.
2.Relations & Functions(20)Periods
Ordered pairs. Cartesian product of sets. Number of elements in the Cartesian product of two finite sets. Cartesian product of the set of reals with itself (upto R x R x R).Definition of relation, pictorial diagrams, domain, co-domain and range of a relation. Function as a special type of relation. Pictorial representation of a function, domain, co-domain and range of a function. Real valued functions, domain and range of these functions, constant, identity, polynomial, rational, modulus, signum, exponential, logarithmic and greatest integer functions, with their graphs. Sum, difference, product and quotients of functions.
3.Trigonometric Functions(20)Periods
Positive and negative angles. Measuring angles in radians and in degrees and conversion from one measure to another. Definition of trigonometric functions with the help of unit circle. Truth of the identity sin2x + cos2x = 1, for all x. Signs of trigonometric functions. Domain and range of trigonometric functions and their graphs. Expressing sin (x±y) and cos (x±y) in terms of sinx, siny, cosx & cosy and their simple applications. Deducing identities like the following: tan(x±y)=tanx±tany1∓tanxtany ,cot(x±y)=cotxcoty ∓1coty±cotxsinα±sinβ=2sin12(α±β)cos12(α∓β) cosα+cosβ=2cos12(α+β)cos12(α−β) 𝑐𝑜𝑠𝛼−𝑐𝑜𝑠𝛽=−2𝑠𝑖𝑛12(𝛼+𝛽)𝑠𝑖𝑛12(𝛼−𝛽) Identities related to sin2x, cos2x, tan2 x, sin3x, cos3x and tan3x.
Unit-II: Algebra
1.Complex Numbers and Quadratic Equations(10)Periods
Need for complex numbers, especially√−1, to be motivated by inability to solve some of the quadratic equations. Algebraic properties of complex numbers. Argand plane
2.Linear Inequalities(10)Periods
Linear inequalities. Algebraic solutions of linear inequalities in one variable and their representation on the number line.
3.Permutations and Combinations(10)Periods
Fundamental principle of counting. Factorial n. (n!) Permutations and combinations, derivation of Formulae for nPr and nCr and their connections, simple applications.
4.Binomial Theorem(10)Periods
Historical perspective, statement and proof of the binomial theorem for positive integral indices. Pascal’s triangle, simple applications.
5.Sequence and Series(10)Periods
Sequence and Series. Arithmetic Mean (A.M.) Geometric Progression (G.P.), general term of a G.P., sum of n terms of a G.P., infinite G.P. and its sum, geometric mean (G.M.), relation between A.M. and G.M.
Unit-III: Coordinate Geometry
1.Straight Lines(15)Periods
Brief recall of two dimensional geometry from earlier classes. Slope of a line and angle between two lines. Various forms of equations of a line: parallel to axis, point -slope form, slope-intercept form, two-point form, intercept form, Distance of a point from a line.
2.Conic Sections(25)Periods
Sections of a cone: circles, ellipse, parabola, hyperbola, a point, a straight line and a pair of intersecting lines as a degenerated case of a conic section. Standard equations and simple properties of parabola, ellipse and hyperbola. Standard equation of a circle.
3.Introduction to Three-dimensional Geometry(10)Periods
Coordinate axes and coordinate planes in three dimensions. Coordinates of a point. Distance between two points.
Unit-IV: Calculus
1.Limits and Derivatives(40)Periods
Derivative introduced as rate of change both as that of distance function and geometrically. Intuitive idea of limit. Limits of polynomials and rational functions trigonometric, exponential and logarithmic functions. Definition of derivative relate it to scope of tangent of the curve, derivative of sum, difference, product and quotient of functions. Derivatives of polynomial and trigonometric functions.
Unit-V Statistics and Probability
1.Statistics(20)Periods
Measures of Dispersion: Range, Mean deviation, variance and standard deviation of ungrouped/grouped data.
2.Probability(20)Periods
Events; occurrence of events, ‘not’, ‘and’ and ‘or’ events, exhaustive events, mutually exclusive events, Axiomatic (set theoretic) probability, connections with other theories of earlier classes. Probability of an event, probability of ‘not’, ‘and’ and ‘or’ events.
Detailed Syllabus [ Class-XI ]
Detailed Syllabus [ Class-XII ]
Unit-I: Relations and Functions
1.Relations and Functions15 Periods
Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions.
2.Inverse Trigonometric Functions 15 Periods
Definition, range, domain, principal value branch. Graphs of inverse trigonometric functions.
Unit-II: Algebra
1.Matrices25 Periods
Concept, notation, order, equality, types of matrices, zero and identity matrix, transpose of a matrix, symmetric and skew symmetric matrices. Operations on matrices: Addition and multiplication and multiplication with a scalar. Simple properties of addition, multiplication and scalar multiplication. Non- commutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2). Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).
2.Determinants 25 Periods
Determinant of a square matrix (up to 3 x 3 matrices), minors, co-factors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of solutions of system of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
Unit-III: Calculus
1.Continuity and Differentiability20 Periods
Continuity and differentiability, chain rule, derivative of inverse trigonometric functions, 𝑙𝑖𝑘𝑒sin−1𝑥,cos−1𝑥and tan−1𝑥, derivative of implicit functions. Concept of exponential and logarithmic functions. Derivatives of logarithmic and exponential functions. Logarithmic differentiation, derivative of functions expressed in parametric forms. Second order derivatives.
2. Applications of Derivatives 10 Periods
Applications of derivatives: rate of change of quantities, increasing/decreasing functions, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).
3. Integrals 20 Periods
Integration as inverse process of differentiation. Integration of a variety of functions by substitution, by partial fractions and by parts, Evaluation of simple integrals of the following types and problems based on them. ∫dx/x2±a2, ∫dx/√x2±a2, ∫dx/√a2−x2, ∫dx/ax2+bx+c, ∫dx/√ax2 +𝑏𝑥+𝑐, ∫px+q/ax2+bx+cdx, ∫px+q/√ax2+bx+cdx, ∫√a2±x2 dx, ∫√x2−a2 dx, ∫√𝑎𝑥2+𝑏𝑥+𝑐 𝑑𝑥,
Fundamental Theorem of Calculus (without proof). Basic properties of definite integrals and evaluation of definite integrals.
4.Applications of the Integrals15 Periods
Applications in finding the area under simple curves, especially lines, circles/ parabolas/ellipses (in standard form only)
5. Differential Equations 15 Periods
Definition, order and degree, general and particular solutions of a differential equation. Solution of differential equations by method of separation of variables, solutions of homogeneous differential equations of first order and first degree. Solutions of linear differential equation of the type:
dy/dx+py=q,where p and q are functions of x or constants.d𝑥/d𝑦+px=q,where p and q are functions of y or constants.
Unit-IV: Vectors and Three-Dimensional Geometry
1. Vectors 15 Periods
Vectors and scalars, magnitude and direction of a vector. Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors.
2. Three - dimensional Geometry 15 Periods
Direction cosines and direction ratios of a line joining two points. Cartesian equation and vector equation of a line, skew lines, shortest distance between two lines. Angle between two lines.
Unit-V: Linear Programming
1.Linear Programming 20 Periods
Introduction, related terminology such as constraints, objective function, optimization, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).
Unit-VI: Probability
1. Probability 30 Periods
Conditional probability, multiplication theorem on probability, independent events, total probability, Bayes’ theorem, Random variable and its probability distribution, mean of random variable.
